Revised 5 September 2023
Accepted 5 October 2023
Available Online 29 November 2023
- DOI
- https://doi.org/10.55060/s.atmps.231115.009
- Keywords
- Umbral methods
Operator theory
Bessel function
Hermite polynomials
Trigonometric functions
Fresnel integral - Abstract
This article presents an overview of Umbral calculus and of its wide range of applicability. The aim is to provide new tools, embedding umbral, symbolic and operatorial methods to be exploited in pure and applied mathematics, in the research of analytical or numerical solutions in different fields.
- Copyright
- © 2023 The Authors. Published by Athena International Publishing B.V.
- Open Access
- This is an open access article distributed under the CC BY-NC 4.0 license (https://creativecommons.org/licenses/by-nc/4.0/).
1. INTRODUCTION
The term Umbra1 has been diffused by S. Roman and G.C. Rota [1] in the second half of the 20th century to underline, in the emerging field of operational calculus, the practice of replacing the representation in series of certain function
To introduce the umbral operator, we have to provide some preliminary definitions. The operator
By that definition, the operator
2. SPECIAL FUNCTIONS
By using the operator in Eq. 25 and the property of
So we have formally reduced a transcendental function to an exponential form, downgrading the “complexity” of the function.
The umbral image is not unique indeed, if we chose another vacuum, the action of the umbral operator will yield a different function. For example, if we introduce the pair umbral operator/vacuum such that:
Example 1.
This kind of new “interpretation” of a certain function opens a wide range of possibilities. To this aim, we provide some examples including the solution of non-trivial integrals.
Example 2.
We consider integrals involving the Bessel function
Furthermore, we want to stress the possibility to evaluate the product of special functions by using the umbral images. However, we recall that in general the operator is not commutative. So if we want to calculate, for example,
By expanding the exponential in MacLaurin series we can finally write:
2.1. Hermite Polynomials
We consider now the two-variable polynomials of Hermite Kampé dè Fériét [4,8,9], also called heat polynomials:
From an operational point of view, they can be expressed as the result of the action of the operator

Geometrical representation of two-variable Hermite polynomials in 3D and 2D for different
Proposition 1.
Proof.
By considering the definition of the
Proposition 2.
The relevant Hermite function integral representation, with order real and negative too, can be written as:
Proof.
By considering the definition of the
Furthermore, if we introduce another application of the umbral methods, called Hermite calculus [15], we can reach the target to combine the previous results and calculate, for example, non-trivial integrals including combination of special functions. To give an idea of the methods we will use, we consider the following integral:
By that position, we can recast:
In this way, we have shown the flexibility of the technique. Indeed, we can raise the complexity of the integrals and solve them by methods as, for example, in the case of the anharmonic oscillator in the example below [15,16].
Example 3.
Let:
be the integral of the anharmonic oscillator. We can solve it by the Hermite calculus position:
in which we used the fractional order of the umbral operator and of the Hermite function:
The same consideration can be done for each special function through appropriate umbral images. We list in the following just some examples for the Laguerre, Jacobi, Legendre, Tricomi-Bessel and Chebyshev functions, and the Voigt transform [12,17,18].
3. NUMBER THEORY
The umbral method can be applied in many different fields of pure and applied mathematics. A further example is indeed Number Theory. We remind that Harmonic Numbers are defined as [19,20,21,22]:
In terms of Laplace transform, we obtain:
We can then introduce the function:
In an analogous way, we can treat other families of numbers like the Motzkin, telegraph, Stirling numbers, etc.
4. CLASSIC TRIGONOMETRY
Trigonometry can also be reinterpreted in terms of umbral images.
Definition 1.
We introduce,
Proposition 3.
(Cos-exponential umbral image) If
Corollary 1.
Fresnel Integral [17]:
By applying the methods discussed so far, we can put together integrals including trigonometric functions and Hermite polynomials [23] and solve them in a simple way.
Example 4.
5. NEW TRIGONOMETRIES AND THE GIELIS SUPERFORMULA
We wish to close this contribution with a view on new trigonometries and the Gielis Superformula.
Definition 2.
We introduce the composition rule
Eq. (42) is based on the Laguerre exponential [24,25]:
Definition 3.
We introduce l-trigonometric (l-t) functions through the identity:
We can also use matrices as arguments of the l-sin or l-cos functions (like in PDE system problems): see Fig. 3.
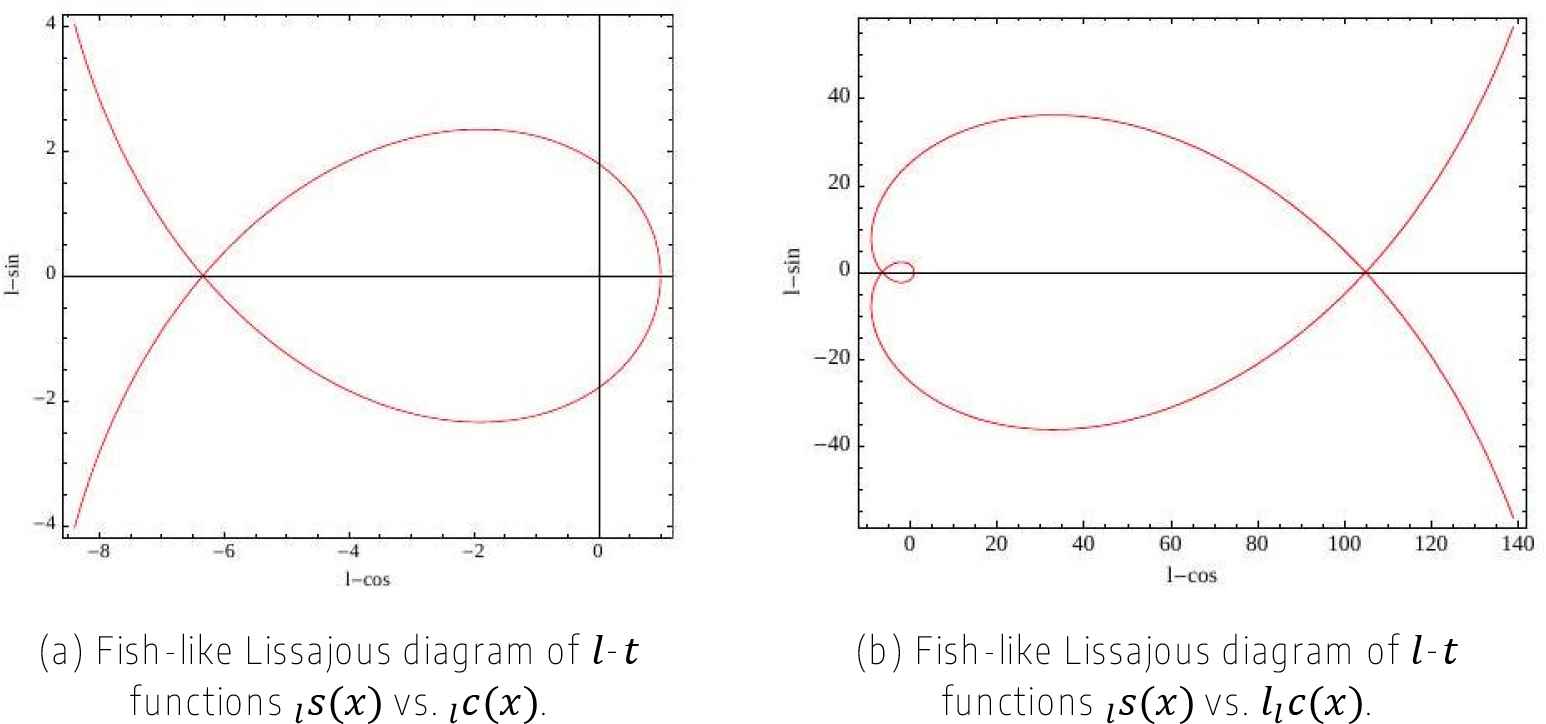
Examples of l-trigonometric functions.
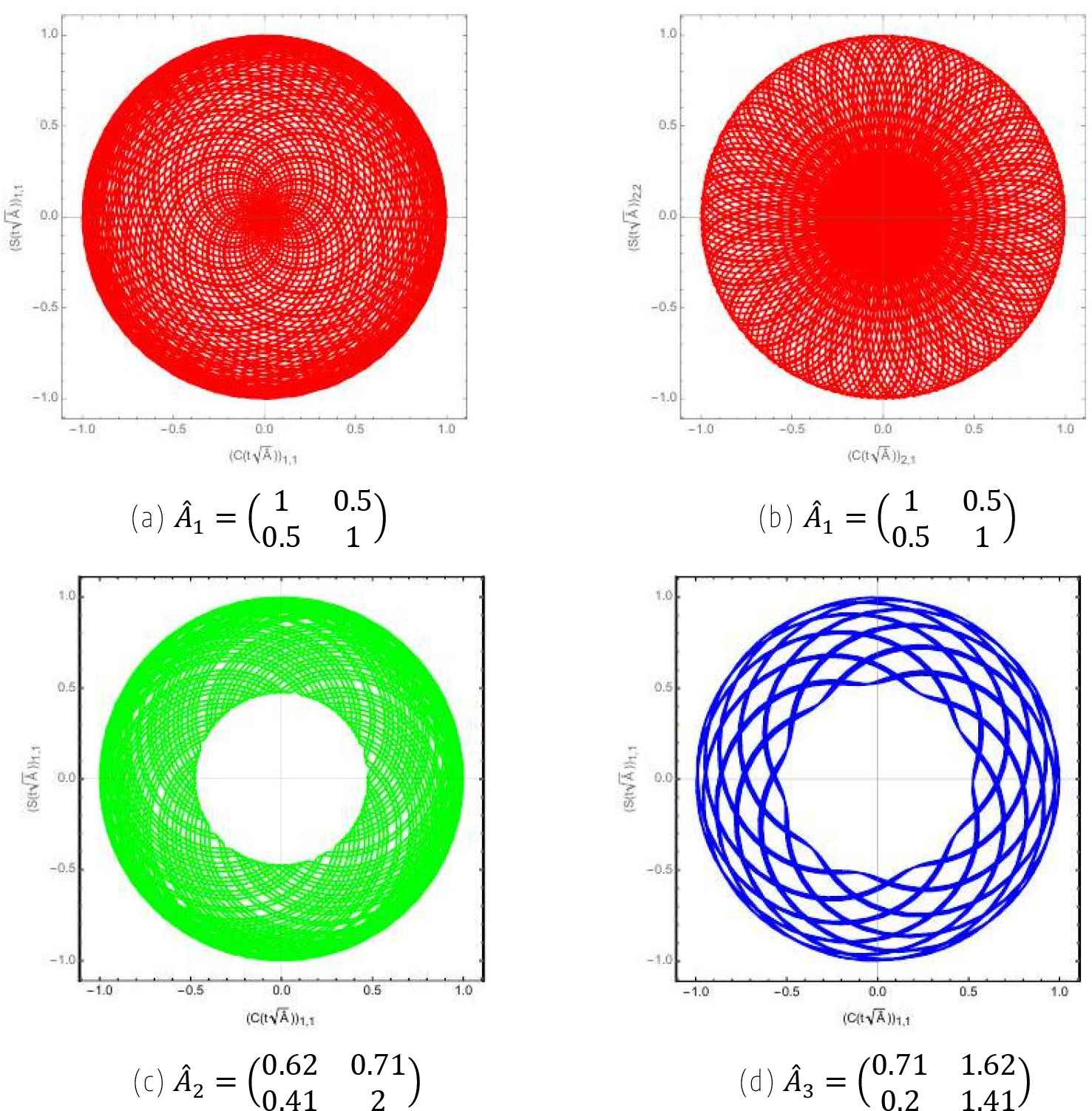
Examples of l-trigonometric functions with matrices as arguments:
Finally, by using the Superformula of Johan Gielis [26], a wide range of novel shapes can be generated (Fig. 4).
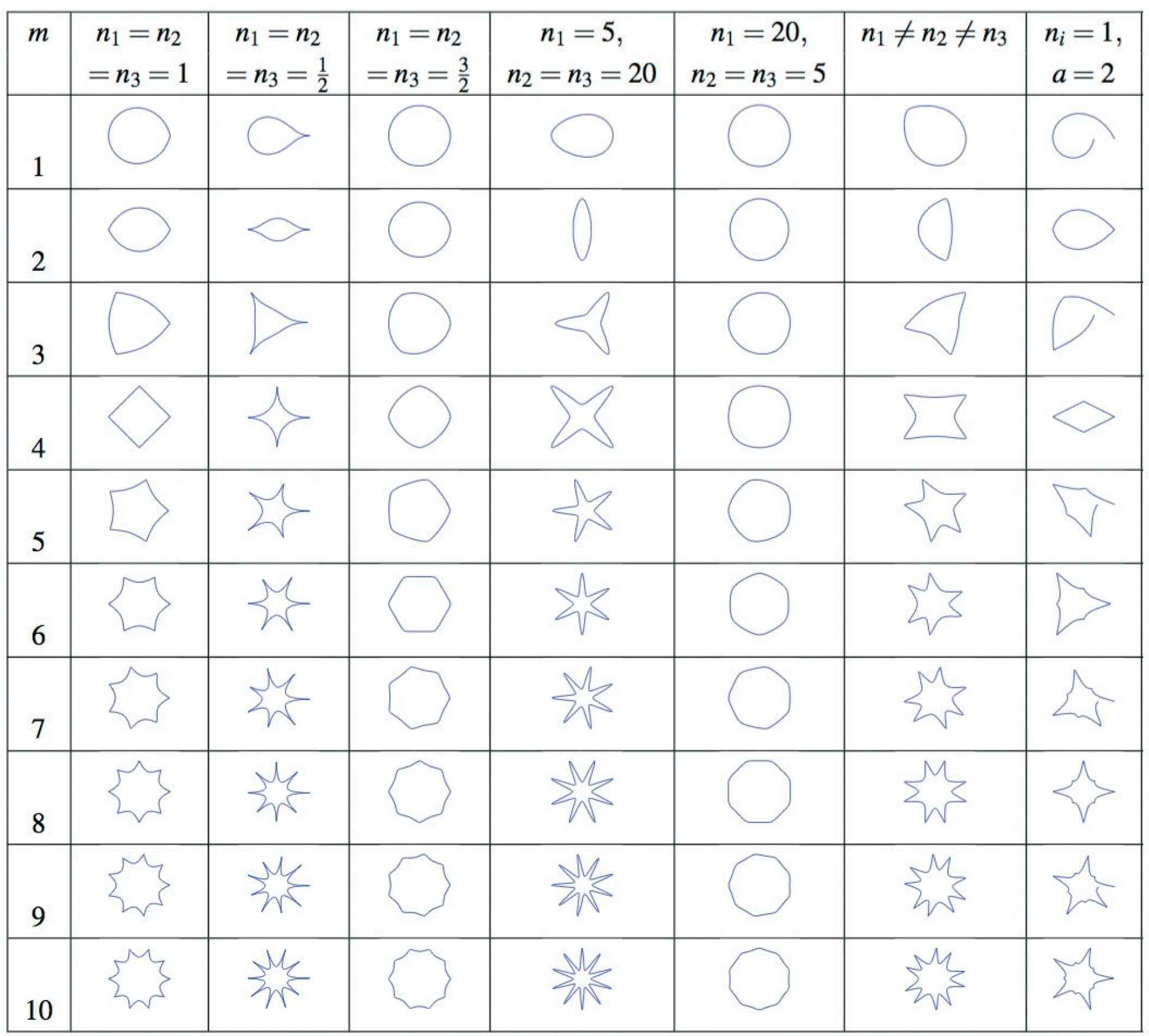
Table of various shapes.
We can identify

(a) Heart. (b) Strange fruit. (c) Strange leaf. (d) Nut. (e) Tulip. (f) Loving hearts.
ACKNOWLEDGMENTS
This work was supported by an ENEA Research Center individual fellowship and under the auspices of INDAM's GNFM (Italy).
Footnotes
It is assonant to the term “Ombra” in Latin which means “shadow” in English.
The promotion of the index n in cn to a power exponent of the operator ĉ, the umbral operator, is the essence of umbra, since it is a kind of projection of one into the other:
This term is used to stress that the action of the operators, raised to some power, is that of acting on an appropriate set of functions by “filling” the initial state
The l-t functions are defined by the corresponding series expansion
REFERENCES
Cite This Article

TY - CONF AU - Silvia Licciardi PY - 2023 DA - 2023/11/29 TI - Umbral Calculus and New Trigonometries BT - Proceedings of the 1st International Symposium on Square Bamboos and the Geometree (ISSBG 2022) PB - Athena Publishing SP - 95 EP - 106 SN - 2949-9429 UR - https://doi.org/10.55060/s.atmps.231115.009 DO - https://doi.org/10.55060/s.atmps.231115.009 ID - Licciardi2023 ER -









